ES242. Data Structures and Algorithms I. Exam 01 - Solutions

ES242. Data Structures and Algorithms I.

Solutions to Exam 01

Issued: 16 Feb, 2023

Remark

The question indices may be different from what you see on Gradescope because of the extra confidence rating questions. Multiply by two and subtract one from the question number to map it to Gradescope :)

Problem 1. The Rubik’s Cube

The Rubik’s Cube is a 3-D combination puzzle involving a cube with a grid of nine squares on each face. In a solved state, each face of the cube has all the nine squares colored using one of six solid colours: white, red, blue, orange, green, and yellow.

The arrangement of colours is now standardised with white opposite yellow, blue opposite green, and orange opposite red, and the red, white, and blue arranged clockwise in that order.

An internal pivot mechanism enables each face to turn independently, thus mixing up the colours. For the puzzle to be solved, each face must be returned to have only one colour.

Suppose you are implementing a Rubik Cube solver. To answer these questions, you do not need to know how to solve a Rubik’s cube. We assume that the cube is in a fixed orientation, so that that we can identify the front, back, top, bottom, left, and right faces in the natural way.

Problem 1.1

One natural way to store the state of the cube is to use six 3x3 arrays of chars, with each character representing a color: cube-front[3][3], cube-back[3][3], cube-top[3][3], cube-bottom[3][3], cube-left[3][3], cube-right[3][3].

In this representation, to get the color of the sticker on the top-left corner of the front face, you would check the value of cube-front[0][0].

In general, for a face F, to get the color of the sticker on row R and column C, you will check the value of cube-F[R][C].

Suppose we have a cube is in some state (not necessarily solved), and we want to transform the state to the one the cube would be in if the top face was rotated clockwise. Which array would remain unchanged?

cube-front[3][3]
cube-back[3][3]
cube-top[3][3]
cube-bottom[3][3]
cube-left[3][3]
cube-right[3][3]

Answer

If the top face is rotated then the bottom face is the only face that is certainly not affected. The top face itself may not be affected (for example, when all stickers on the top face have the same color), however, this is not guaranteed.

Problem 1.2

Consider the following approach. Instead of storing six separate two-dimensional arrays, we store the state of the cube as a linked list with 54 entries as depicted below, by listing all the elements in the cube-front array first, followed by cube-back, cube-top, cube-bottom, cube-left, cube-right. The elements within a face are listed row-wise (i.e, all elements of the first row are listed first, second row second, and so on).

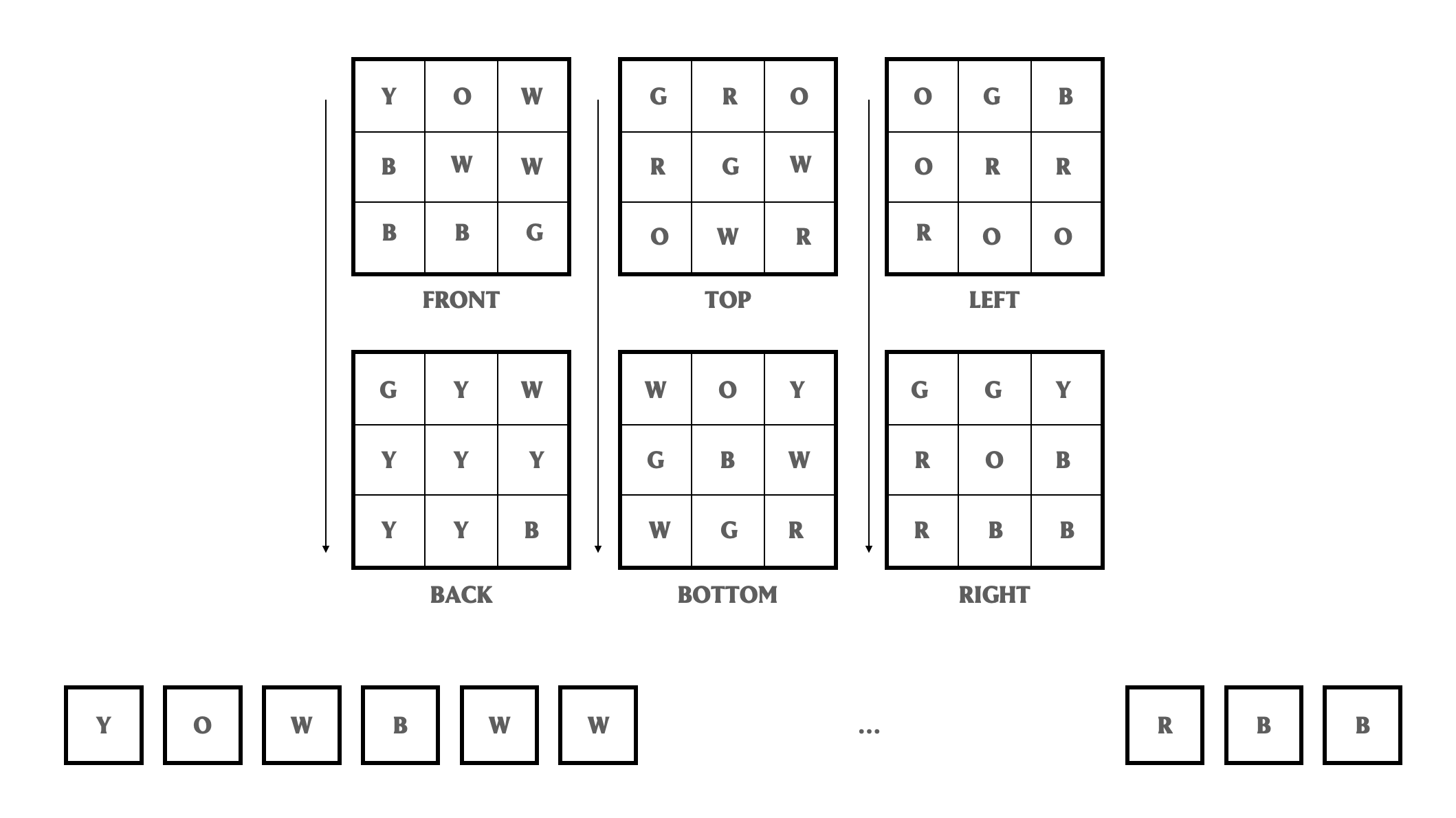
Transforming the arrays to a linked list

Suppose you want to determine the color of a sticker at a particular location, which is specified by the face, row number, and column number. Which approach will require more steps?

The array approach
The linked list approach

Answer

While the index of the location in the linked list can be calculated in constant time, since we do not have direct access, the linked list approach will require more steps in the worst case.

Problem 1.3

Consider the linked list approach from the previous question. What is the index of the element that stores the color of the center sticker (i.e, row 1 and column 1 with 0-based indexing) of the bottom face? Assume that the linked list is 1-indexed: for example the index of the element that stores the color of the center sticker for the front face is 5.

Answer

The answer is 32 by direct inspection.

Problem 1.4

Observe that the central pieces of each face in a Rubik’s cube do not move with any of the rotations. We can think of the Rubik’s cube as being assembled from 8 corner pieces and 12 edge pieces as shown below. Each of these individual pieces is called a cubie.

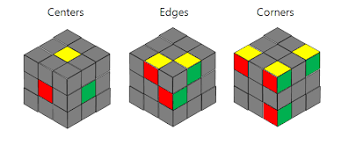
Observe that the state of the cube can be fully specified by specifying the orientation of all the cubies. Fix a labeling of all the corner cubies from 0 to 7 and the edge cubies from 0 to 11.

In particular, let us say that we store the state by storing two orientation arrays and two location arrays.

The first array, C stores the orientation of the corner cubies and the second array E, stores the orientation of edge cubies. The elements of each array stores an orientation (0 or 1 for edges; 0, 1, or 2 for corners).

The third array, CC stores the location of the corner cubies and the fourth array EE, stores the location of edge cubies. The elements of CC are values between 0 and 7 and the elements of EE are values between 0 and 11.

The state can be recovered from the orientations of all the cubies: for example, we know that the edge cubie with label 3 is at the location EE[3], and oriented according to the value stored in E[3].

Which data structure for representing the state of a Rubik’s cube takes up the least space? Assume that we are measuring the space in terms of the total lengths of the sequences involved in each representation.

the first approach with six 2D arrays
the second approach using a linked list
the current approach using two cubie arrays

Answer

The cubie approach requires employing a total of 40 units of memory, which is less than the 54 units we needed in the other two approaches.

Problem 1.5

Consider the representation involving cubies described in the previous part.

Suppose we have a cube is in some state (not necessarily solved), and we want to transform the state to the one the cube would be in if the top face was rotated clockwise. How many values would you have to update in the CC array?

Answer

Since only four corner cubes are involved in one rotation, the answer is 4. Note that the set of affected cubies is the same for 90 and 180 degree rotations of the top face.

Problem 1.6

Consider the representation involving cubies described in the previous part.

Answer

Since only four edge cubes are involved in one rotation, the answer is 4. Note that the set of affected cubies is the same for 90 and 180 degree rotations of the top face.

Problem 2. Stable Matchings

Recall that the stable matching problem involves N men and N women. Each man has a ranking of all N women and each woman has a ranking of all N men. A matching M is a collection of N pairs where each pair consists of a man and a woman, and all the men and women appear in exactly one pair. A man a and a woman b are said to block M if a prefers b over his matched partner in M and b prefers a over her matched partner in M according to their respective rankings. A matching is stable if there are no blocking pairs with respect to it.

Problem 2.1

Suppose X and Y are two stable matchings. For a man a, let X[a] denote the matched partner of a in the matching X and let Y[a] denote the matched partner of a in the matching Y.

Consider a matching Z formed as follows: pair up each man a with the woman he prefers more between X[a] and Y[a].

Note: If X[a] and Y[a] happen to be the same woman b, then pair a with b.

What can we say about Z?

Z is not necessarily a matching.
Z is a matching but not necessarily stable.
Z is always a stable matching.

Answer

First, let us argue that Z is a matching. Suppose not: this means that some woman appears in more than one pair. Suppose there are two men p and q who are both matched to a woman b. Then p and q both prefer b over their matched partners in the matching where they are not matched to b. Now:

If b prefers p over q, and p was matched to b in the matching X, then observe that b must have been matched to q in Y and (p,b) is a blocking pair for Y.
If b prefers p over q, and p was matched to b in the matching Y, then observe that b must have been matched to q in X and (p,b) is a blocking pair for X.
If b prefers q over p, and q was matched to b in the matching X, then observe that b must have been matched to p in Y and (q,b) is a blocking pair for Y.
If b prefers q over p, and q was matched to b in the matching Y, then observe that b must have been matched to p in X and (q,b) is a blocking pair for X.

In all cases, we have a contradiction to the assumption that both X and Y are stable.

So Z is a matching. We now argue that Z is stable. Suppose not, and let (a,b) be a blocking pair in Z, with a being the man and b being the woman. Further, let the matched partner of a in Z be p and the matched partner of b in Z be q.

Note that b was matched to q in either X or Y. Suppose b was matched to q in X. In X, a is matched either to p or someone that a prefers less to p. Since a prefers b over p (since (a,b) is a blocking pair), a prefers b over his matched partner in X. We already know that b prefers a over q for the same reason. So, (a,b) remains a blocking pair in the matching X, which contradicts our assumption that X was stable.

A similar argument holds if b was matched to q in Y, where we contradict the stability of Y instead.

Problem 2.2

Suppose X and Y are two stable matchings. For a man a, let X[a] denote the matched partner of a in the matching X and let Y[a] denote the matched partner of a in the matching Y.

Consider a matching Z formed as follows: pair up each man a with the woman he prefers less between X[a] and Y[a].

Note: If X[a] and Y[a] happen to be the same woman b, then pair a with b.

What can we say about Z?

Z is not necessarily a matching.
Z is a matching but not necessarily stable.
Z is always a stable matching.

Answer

It turns out that Z is always a stable matching, the argument is analogous to the previous question.

Problem 3. An Array and A Virus

The memory of Rubina’s computer contains two interesting things: an array of integers and a virus. Each midnight the virus becomes active. It takes each array in memory and replaces it with a bunch of new arrays: one for each contiguous subarray of the original array.

For example, if today the memory contains a single array (1,2,1,3), tomorrow it will contain the following arrays: (1), (2), (1), (3), (1,2), (2,1), (1,3), (1,2,1), (2,1,3), (1,2,1,3).

As another example, if today the memory contains a single array (7,7), tomorrow it will contain the following arrays: (7), (7), (7,7), and the day after tomorrow it will contain the following arrays: (7), (7), (7), (7), (7,7), and so on.

You are given Rubina’s original array A and the number of days D. Let f(A,D) be the sum of all elements of all arrays that will be in the memory of Rubina’s computer after D days. Our goal is to calculate f(A,D). You may assume that the memory of Rubina’s computer is sufficiently large to accommodate all the arrays.

For example, if A is the array (1,2,1,3) and D = 0 then the answer is 7.

Problem 3.1

If A = (1,2,1,3) and D = 1, what is f(A,D)?

Answer

Problem 3.2

If A = (500) and D = 120, what is f(A,D)?

Answer

500

Problem 3.3

If A = (1,2) and D = 10, what is f(A,D)?

Answer

Problem 3.4

If A has four elements, how many arrays of length one are there after two steps?

Answer

Problem 4. A Bit of a Graph

The bit strings of length four are given by:

0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111.

Consider a graph where we have:

a vertex for every bit string of length four, and let us say that the bit string associated with a vertex u is denoted by b_u; and
an edge from u to v if the corresponding bit strings are such that the last three bits of b_u is the same as the first three bits of b_v.

For example, we will have an edge from the vertex representing 0010 to the vertex representing 0101. We will also have an edge from the vertex representing 0010 to the vertex representing 0100.

Problem 4.1

How many vertices does this graph have?

Answer

Problem 4.2

How many edges does this graph have?

Answer

Problem 4.3

How many vertices in this graph have a self-loop?

Answer

Two

Problem 4.4

Does this graph have a closed Euler Tour?

Answer

Yes