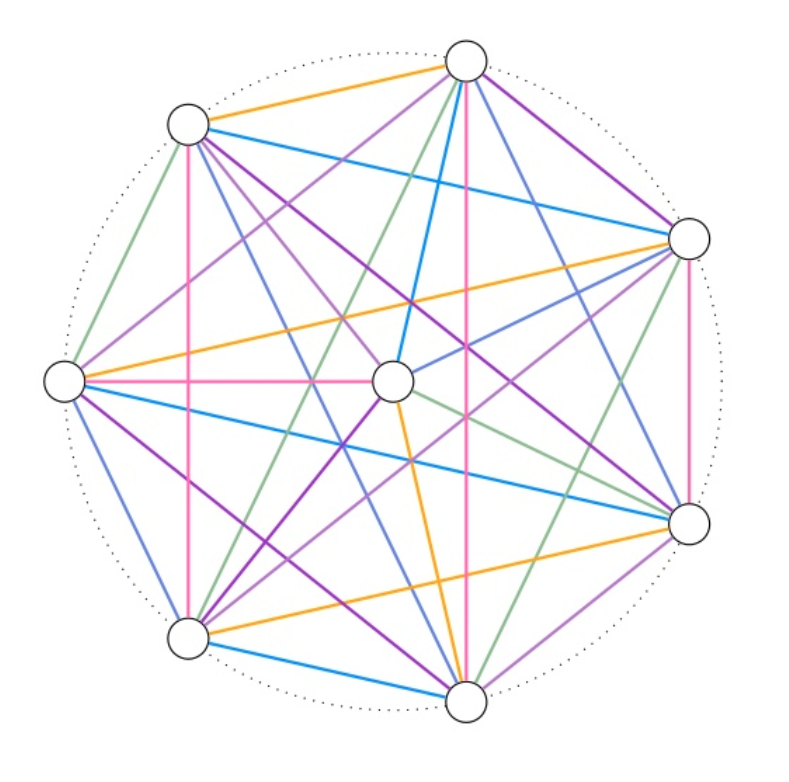
Visualizing Baranyai’s theorem for the case when n=2.

Neeldhara Misra

Smt. Amba and Sri. V S Sastry Chair Associate Professor
Computer Science and Engineering at IIT Gandhinagar
(she/her)

My broad research interests include — in no particular order: algorithm design, computational social choice, combinatorial games. You can find out more about my work here.

Recent PCs: FSTTCS 2024 (also co-organizing), Compute 2024 (also co-organizing), IJCAI 2024, ADT 2024, CALDAM 2024, FUN 2024, IWOCA 2024, IJCAI 2024, AAMAS 2023, CALDAM 2023, FSTTCS 2023, FUN 2022, MFCS 2022, IPEC 2022, IJCAI 2022, Compute 2022, CALDAM 2023, IPEC 2023 (co-chair with Magnus Wahlström)

Latest News

CompEd 2023 Doctoral Symposium | Aug 1, 2023

CompEd will be held between December 7-9, 2023, at Hyderabad, India, and will feature a Doctoral Consortium. Check out the call for entries! The deadline for making a submission is Monday, 21 August 2023.

The Price of Equity with Binary Valuations and Few Agent Types | Jul 10, 2023

Joint work with Umang Bhaskar, Aditi Sethia, and Rohit Vaish ⸱ To Appear at SAGT 2023 ⸱ ArXiV

In fair division problems, the notion of price of fairness measures the loss in welfare due to a fairness constraint. Prior work on the price of fairness has focused primarily on envy-freeness up to one good (EF1) as the fairness constraint, and on the utilitarian and egalitarian welfare measures. Our work instead focuses on the price of equitability up to one good (EQ1) (which we term price of equity) and considers the broad class of generalized p-mean welfare measures (which includes utilitarian, egalitarian, and Nash welfare as special cases). We derive fine-grained bounds on the price of equity in terms of the number of agent types (i.e., the maximum number of agents with distinct valuations), which allows us to identify scenarios where the existing bounds in terms of the number of agents are overly pessimistic.

Our work focuses on the setting with binary additive valuations, and obtains upper and lower bounds on the price of equity for p-mean welfare for all p <= 1. For any fixed p, our bounds are tight up to constant factors. A useful insight of our work is to identify the structure of allocations that underlie the upper (respectively, the lower) bounds simultaneously for all p-mean welfare measures, thus providing a unified structural understanding of price of fairness in this setting. This structural understanding, in fact, extends to the more general class of binary submodular (or matroid rank) valuations. We also show that, unlike binary additive valuations, for binary submodular valuations the number of agent types does not provide bounds on the price of equity.

Spartan Bipartite Graphs are Essentially Elementary | Jul 1, 2023

Joint work with Saraswati Nanoti ⸱ To Appear at MFCS 2023 ⸱ Preprint coming soon!

We study a two-player game on a graph between an attacker and a defender. To begin with, the defender places guards on a subset of vertices. In each move, the attacker attacks an edge. The defender must move at least one guard across the attacked edge to defend the attack. The defender wins if and only if the defender can defend an infinite sequence of attacks. The smallest number of guards with which the defender has a winning strategy is called the eternal vertex cover number of a graph G and is denoted by evc(G). It is clear that evc(G) is at least mvc(G), the size of a minimum vertex cover of G. We say that G is Spartan if evc(G) = mvc(G). The characterization of Spartan graphs has been largely open. In the setting of bipartite graphs on 2n vertices where every edge belongs to a perfect matching, an easy strategy is to have n guards that always move along perfect matchings in response to attacks. We show that these are essentially the only Spartan bipartite graphs.

Finding Perfect Matching Cuts Faster | Mar 27, 2023

Joint work with Yash More ⸱ To Appear at IWOCA 2023 ⸱ Preprint coming soon!

A cut (X,Y) is a perfect matching cut if and only if each vertex in X has exactly one neighbor in Y and each vertex in Y has exactly one neighbor in X. The computational problem of determining if a graph admits a perfect matching cut is NP-complete, even when restricted to the class of bipartite graphs of maximum degree 3 and arbitrarily large girth. We demonstrate a faster exact exponential time algorithm on general graphs and an even faster algorithm on graphs of maximum degree three that have girth six.

CompEd 2023 Dates Announced | Mar 24, 2023

CompEd will be held between December 7-9, 2023, at Hyderabad, India. Check out the call for participation! The deadline for submitting abstracts is Sunday, 7 May.

IPEC 2023 Dates Announced | Mar 20, 2023

The International Symposium on Parameterized and Exact Computation (IPEC) is an annual conference covering all aspects of parameterized and exact algorithms and complexity. Its 18th edition will be part of ALGO 2023, which also hosts ESA 2023 and other specialized conferences and workshops. We are excited that ALGO 2023 is planned as an in-person conference and we look forward to seeing you there! ALGO will be held between September 4-8, 2023, at Amsterdam, the Netherlands.

Do submit your best work to IPEC 2023 --- the abstract submission deadline is June 27th (23:59 AoE).

NASI Platinum Jubilee Young Scientist Award | Jan 5, 2023

Recieved the NASI Platinum Jubilee Young Scientist Award. Most grateful to all collaborators and mentors who make this recognition possible.

All News

Latest Posts

10 May, 2024	Creating a Gallery of Solved Crosswords	workflows
13 Jan, 2024	Winning	poem
01 Jan, 2024	Poetry	poem
25 Dec, 2023	Course Plan Generator	workflows
25 Dec, 2023	Course Plan Generator	workflows
21 Dec, 2023	Intro to Crypto	talk exposition
01 Oct, 2023	Exportober 2023	workflows

All Posts

In case you care for (sporadic) updates by email.

I mostly plan to write some notes to self: I can’t imagine that you’d be interested, but if, for some reason, you are, you are welcome.