CS614. Advanced Algorithms. Exam 1.

CS614. Advanced Algorithms.

Exam 3

EXACT MATCH (3 points)

Given a graph $G$ and an integer $k$ , the EXACT MATCH problem asks for an induced matching of size $k$ , that is, $k$ edges $x_1 y_1, \ldots, x_k y_k$ such that the $2k$ endpoints are all distinct and there is no edge between $\left\{x_i, y_i\right\}$ and $\left\{x_j, y_j\right\}$ for any $i \neq j$ .

Prove that EXACT MATCH parameterized by $k$ is as hard as INDEPENDENT SET parameterized by $k$ .

Dominating Set on Restricted Classes

Consider the Dominating Set problem.

Problem 2.1 Understanding graph classes (1 point)

Let $\mathcal{A}$ be the graphs excluding the star $K_{1,4}$ as an induced subgraph. That is, a graph $G$ belongs to $\mathcal{A}$ if and only if there is no copy of a star on four leaves as an induced subgraph (but you may still have vertices of degree four or more).

Similarly, let $\mathcal{B}$ be the graphs excluding the star $K_{1,2}$ as an induced subgraph.

Which of the following is true?

$\mathcal{A} \subseteq \mathcal{B}$
$\mathcal{B} \subseteq \mathcal{A}$
neither of the above

Problem 2.2 An Easy Case (2 points)

Can you solve Dominating Set in polynomial time if your input graph does not contain the star $K_{1,2}$ as an induced subgraph?

Problem 2.3 A Hard Case (4 points)

Prove that Dominating Set restricted to graphs excluding the star $K_{1,4}$ as an induced subgraph is as hard as Dominating Set on general graphs.

Hint: look up the textbook (Theorem 13.15) reduction for Connected Dominating Set and adapt it.

PERMUTATION COMPOSITION (3 points)

The EXACT UNIQUE HITTING SET problem is the following:

Input: A universe $U$ , a set $A$ of subsets of $U$ , and an integer $k$ . Question: Does there exist a set $X \subseteq U$ of size exactly $k$ such that $|A \cap X|=1$ for every $A \in A$ ?

In the PERMUTATION COMPOSITION problem, the input consists of a family $\mathcal{P}$ of permutations of a finite universe $U$ , additional permutation $\pi$ of $U$ , and an integer $k$ , and the question is whether one can find a sequence $\pi_1, \pi_2, \ldots, \pi_k \in \mathcal{P}$ such that:

$\pi=\pi_1 \circ \pi_2 \circ \ldots \circ \pi_k.$

Show a reduction from EXACT UNIQUE HITTING SET to PERMUTATION COMPOSITION.

NICE SUBSET (3 points)

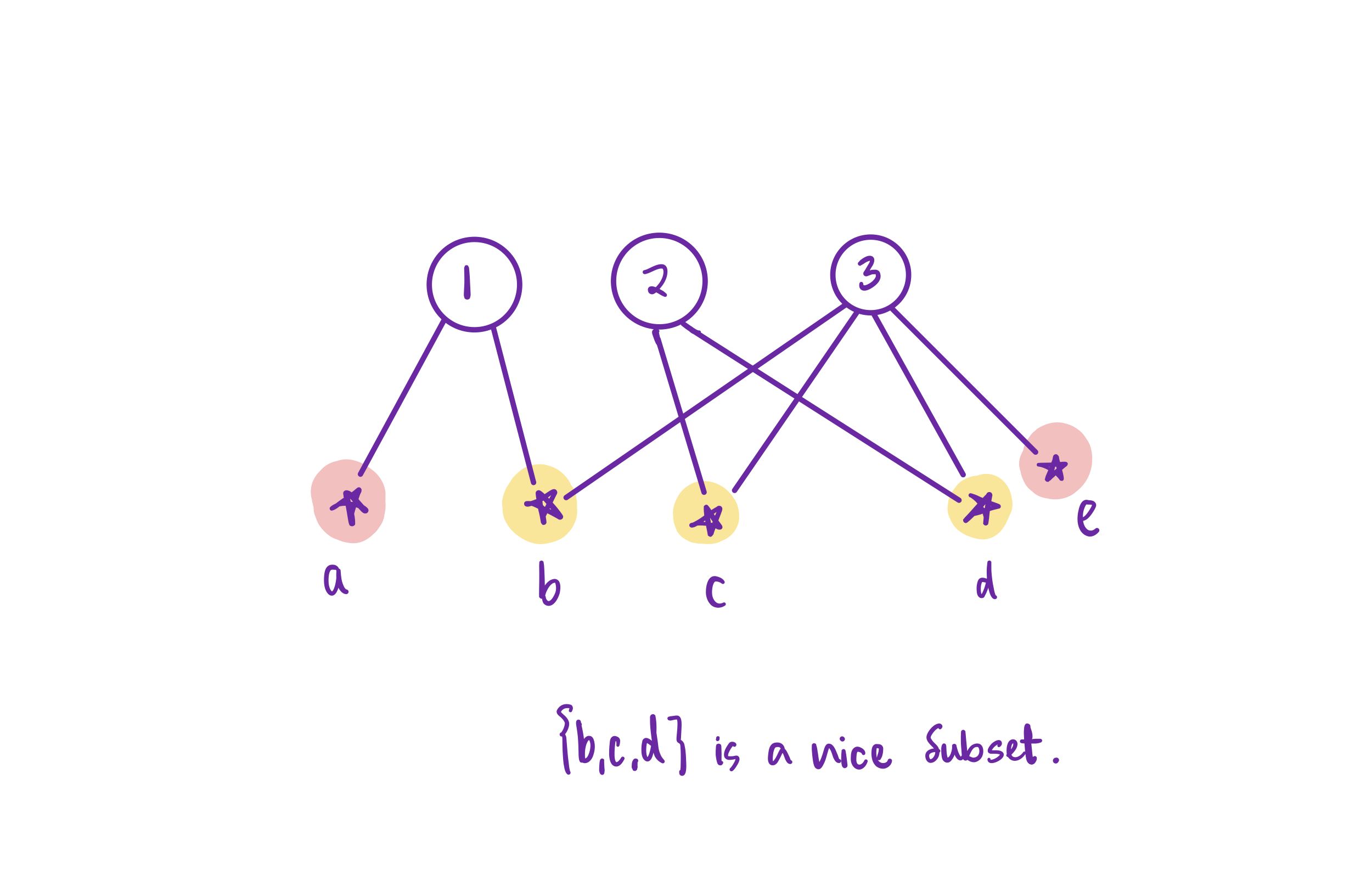
Let $G=\left(X, Y, E\right)$ be an undirected bipartite graph, that is, a graph whose nodes are divided into two sets, $X$ and $Y$ , such that every edge in $E$ connects a node in $X$ to a node in $Y$ . The nodes in $X$ are all labeled with non-negative integers.

Some of the nodes in $Y$ can be removed to leave a subset $W \subseteq Y$ . A subset $W$ is called nice with $G$ if every node in $X$ which has been assigned a number $m$ is connected to exactly $m$ nodes in $W$ . An example of a nice set is in the image below.

The problem is to determine whether a nice $W$ exists. Demonstrate a reduction from 3SAT to this problem.

NP-completeness Examples (4 points)

Pick any two problems below and show that they are NP-complete.

Problem 5.1

Given an undirected graph $G$ , does $G$ contain a simple path that visits all but 9 vertices?

Problem 5.2

Given an undirected graph $G$ , does $G$ have a spanning tree in which every node has degree at most 32?

Problem 5.3

Given an undirected graph $G$ , does $G$ have a spanning tree with at most 5 leaves?

Problem 5.4

Given an undirected graph $G=(V, E)$ , what is the size of the largest subset of vertices $S \subseteq V$ such that at most 50 edges in $E$ have both endpoints in $S$ ?