Dog Bunny Puzzle

Dog Bunny: A Cute Puzzle

Conrad Barski (@lisperati)’s latest, Dog Bunny Puzzle, had jumped to #1 on HN. The puzzle presents the following somewhat minimalist interface:

The Dogs Bunny Puzzle

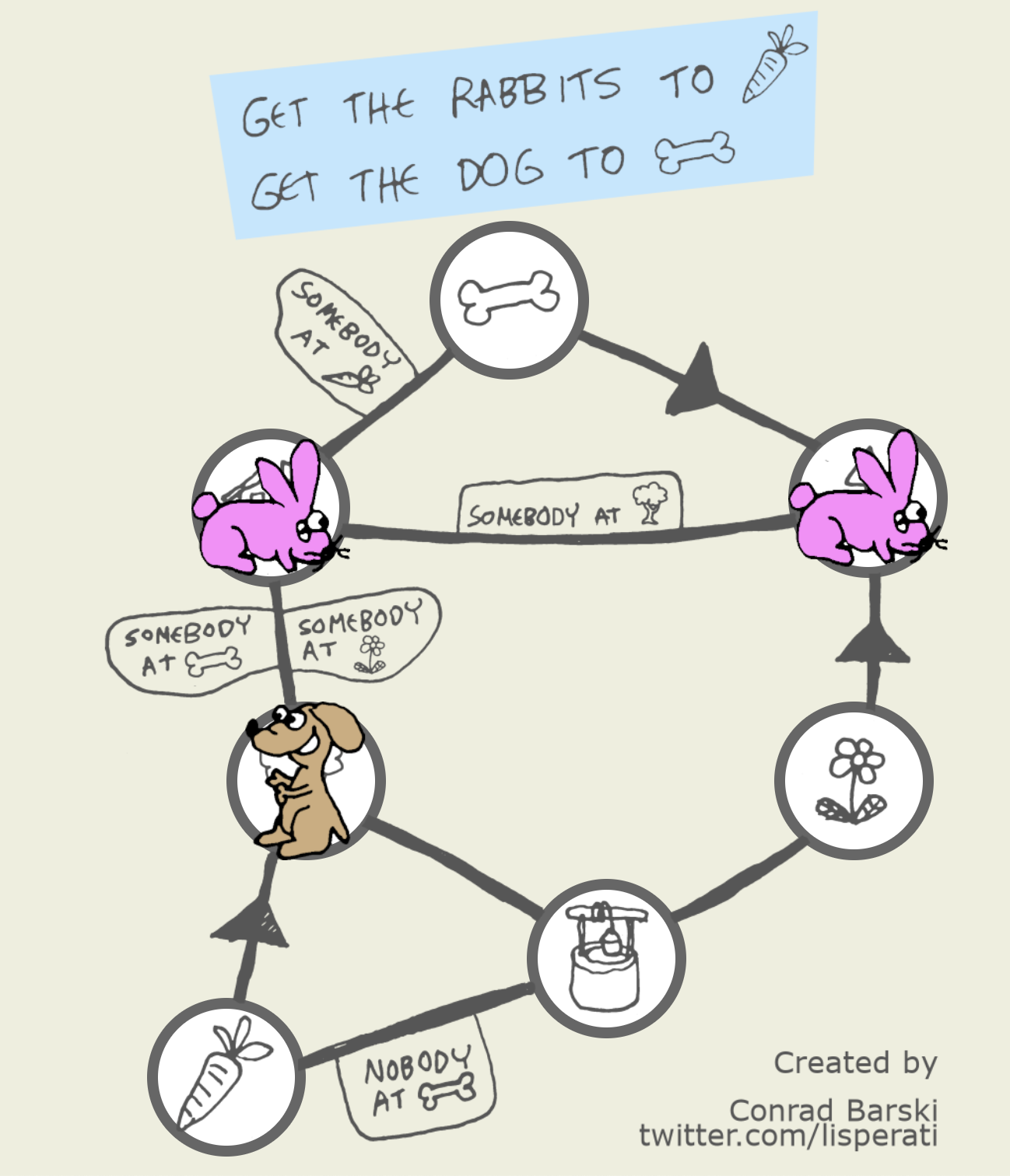
If you haven’t played it yet, you might want to go ahead and give it a shot first. Most people figured out the mechanics without any explicit instructions. A couple of things that may not be immediately clear, but typically discovered quickly within a few moves:

• The edges are labeled with conditions, and can be used only if all of the said conditions are met.

• The bunny or dog icons may sometimes cover up what kind of location they are at. You can drag them away to find out!

• Multiple animals can occupy the same spot at a time.

• It is possible to get into a dead end, a situation from where no legal moves are possible. In the verison of the game that is available at the time of this writing, the game offers no sign that you might be in this situation. This may however change.

After winging it on the puzzle, several questions seemed natural:

What’s the smallest number of moves to win?

Apparently 26.

Can you write a program to find a solution?

Yes (Python) and yes (Picat).

Can a script generate more of these puzzles?

Indeed:

For those paying attention, yes I am two days late :(

FYI, I also have a program now that can create an infinite number of these puzzles at differing difficulty

How would you rate the puzzle I posted today?

— Conrad Barski (@lisperati) September 17, 2022

Are there connections with other well-known puzzles?

Why yes, check out the Wolf puzzle (as pointed out by @RianNeogi) and this Numberphile video about it.

Is the problem NP-complete?

Before you ask, I am not the only one who’s asking!

So the last question may strike you as a bit left-field, but that’s what I’m going to ramble about for the rest of this post :) It turns out that the answer is in the affirmative, and here is a lovely reduction by @lokshtanov showing as much.

The Reduction

Let’s just set up the game as a computational problem just to be sure that we agree on the abstraction. In fact, we’ll be working with a simpler version that we will call BunnyCarrot.

BunnyCarrot

In the BunnyCarrot problem, the input is a simple undirected graph $G = (V,E)$, subsets $B$ and $C$ of $V$ indicating the initial positions of bunnies and carrots, and a (possibly empty) instruction $r_e$ for every $e \in E$, which is a collection of conditions, at least one† of which must be true for the edge $e$ to be “active”.

The question is if there is a sequence of movements of bunnies along active edges such that at the end of the sequence, every bunny is located at one of the vertices from $C$.

† In the original version of the problem, we need all conditions associated with an edge to be satisfied, not at least one. The construction that we will describe can be easily adapted to this setting as well, but is simpler to describe for this variant :)

We are going to show that BunnyCarrot is NP-complete by reducing from 3SAT. So let $\phi := \{C_1, \ldots, C_m\}$ be a collection of $m$ 3SAT clauses over variables $\{x_1, \ldots, x_n\}$. The reduced instance of BunnyCarrot corresponding to $\phi$ looks like this:

A cartoon sketch of the reduced instance of BunnyCarrot from 3SAT.

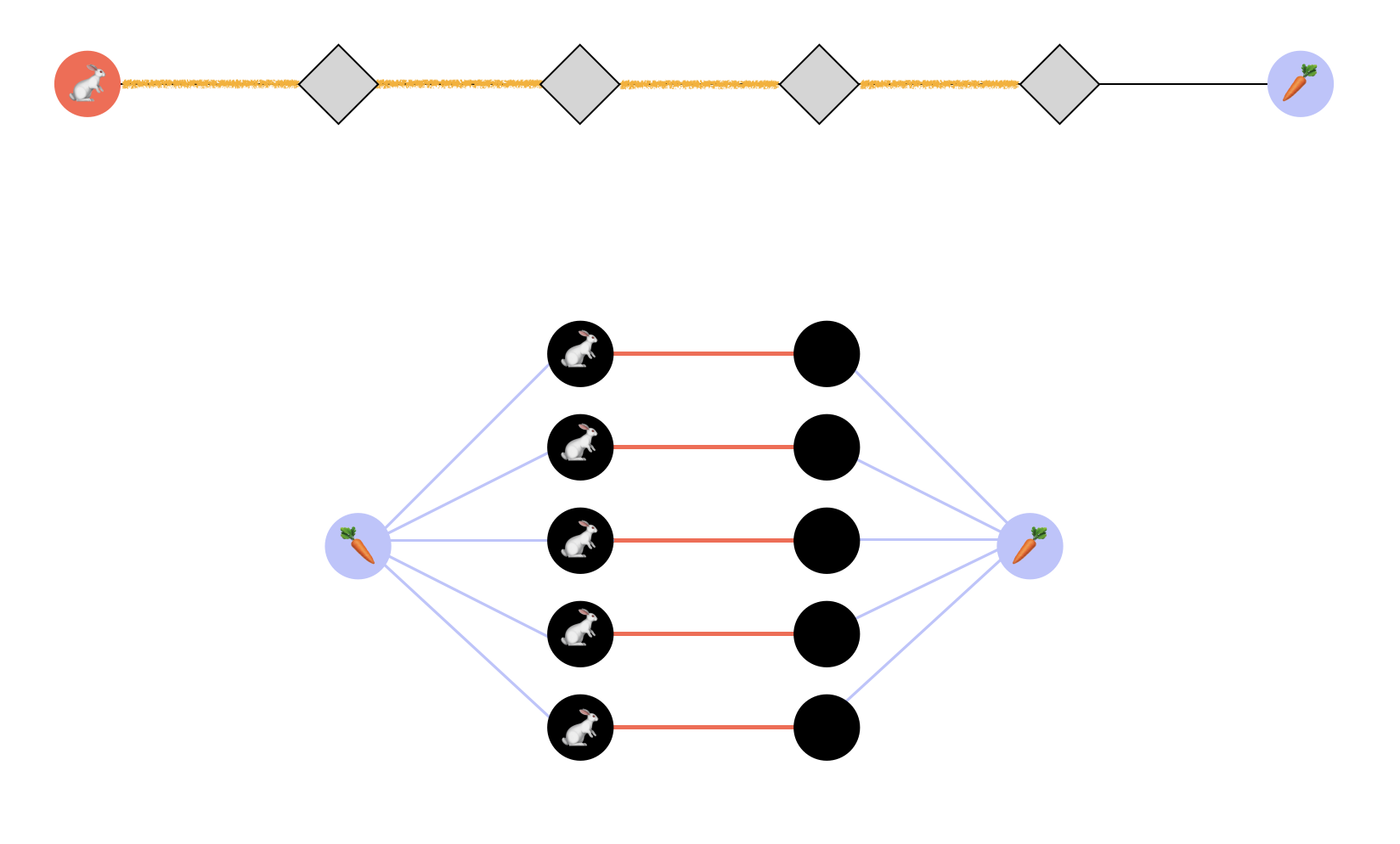
What we have here is the following in terms of the structure of graph:

• a path $X$ on $m+2$ vertices, with the left most vertex in $B$ and the rightmost one in $C$;

• a pair of vertices $(u_i,v_i)$ for every $i \in [n]$, and an edge between them, where all the $u_i$’s are in $B$’ — the vertex $u_i$ represents the literal $x_i$ while the vertex $v_i$ represents the literal $\overline{x_i}$;

• a pair of vertices $p$ and $q$ in $C$, with $p$ adjacent to all $u_i$’s and $q$ adjacent to all $v_i$’s.

Now here be the instructions associated with the edges:

• the edge to the $\ell$-th vertex on $X$ is active only if there is a bunny on at least one of the literals present in the clause $C_{\ell-1}$;

• the edges between $u_i$ and $v_i$ are active only when there is a bunny on the leftmost vertex of $X$; and

• finally, the edges incident on $p$ and $q$ are active only when there is a bunny on the rightmost vertex of $X$.

The Forward Direction

We first claim that we can “win” this game if $\phi$ has a satisfying assignment. Indeed, let $$\tau: \{x_1,\ldots,x_n\} \rightarrow \{0,1\}$$ be a truth assignment that satisfies all the clauses of $\phi$. Then:

1. If $\tau(x_i) = 0$, move the bunny on $u_i$ to $v_i$.

2. Move the bunny on the leftmost vertex of the path $X$ to the rightmost vertex: note that all edges are active because $\tau$ is a satisfying assignment.

3. Move all bunnies on $u_i$’s to $p$ and those on $v_i$’s to $q$.

The Backward Direction

Now suppose there is a winning sequence of moves $\sigma$. We will show that we can extract from this sequence a satisfying assignment for $\phi$, which will firmly establish the equivalence of the generated instance of BunnyCarrot with the OG hard instance $\phi$.

Note that to begin with, all the blue edges are inactive. Now, in the sequence $\sigma$, let us say that a step is key if it involves a bunny moving along the first edge of the path $X$ and critical if it involves a bunny moving along the last edge of the path $X$.

Suppose the $\ell$-th step is the first critical step in $\sigma$. Further, suppose that the $t$-th step is the last key step to occur before the $\ell$-th step. Notice that there must be at least one key step before a critical step — we must begin before we can end :)

Now, for all steps after the $t$-th step and before the $\ell$-th step, note that edges incident to $u_i$ and $v_i$ are inactive for all $i \in [n]$. This implies that every step between the $t$-th and $\ell$-th steps involves a bunny moving along $X$, and in particular, every edge in $X$ is crossed at least once in this phase of the game.

Let us note the positions of the bunnies who are on the $u_i$’s and $v_i$’s after the $t$-th step is executed. Observe that this naturally translates to an assignment on the variables as follows:

$$\begin{equation*} \tau(x_i) = \begin{cases} 1 & \text{if } u_i \in B,\\ 0 & \text{if } v_i \in B. \end{cases} \end{equation*}$$

We argue that $\tau$ must in fact be a satisfying assignment.

Assume to the contrary: suppose some clause $C_k$ is, in fact, not satisfied by $\tau$.

Then, we claim that the edge connecting the $k$-th and $(k+1)$-th vertices is not active.

As an example, suppose $C_k = \{x_1,x_2,\overline{x_3}\}$. Since $\tau$ does not satisfy $C_k$, it must be the case that:

• $\tau(x_1) = 0$ — and hence there is a bunny on $v_1$;
• $\tau(x_2) = 0$ — and hence there is a bunny on $v_2$;
• $\tau(x_3) = 1$ — and hence there is a bunny on $u_3$.

However, the condition for the edge to the $(k+1)$-th vertex on $X$ to be active is simply that there is a bunny present on at least one of the literals present in the clause $C_{k}$, i.e, one of $u_1$, $u_2$ or $v_3$. However, because of the structure of the graph, and the fact that all edges incident on $p$ and $q$ are inactive at all times before the first critical step, observe that:

• If there is a bunny on $v_1$, there is no bunny on $u_1$.
• If there is a bunny on $v_2$, there is no bunny on $u_2$.
• If there is a bunny on $u_3$, there is no bunny on $v_3$.

By our assumption that $\tau$ falsifies $C_k$, all the premises above are true! So there is an edge on the path $X$ that is not active between the $t$-th and $\ell$-th steps, which violates our understanding that every edge was crossed between these steps. This is a contradiction, and hence $\tau$ must indeed be a satisfying assignment.

I’ll just remark here that this construction can be modified so that every vertex in the graph has constant degree, and there is only one vertex in $C$. It can also be modified to change the “or” condition on the edges to an “and”, by simply separating the conditions out along multiedges.

Food for thought

Here are some more questions :)

1. What’s the complexity of this game when the underlying graph has some simple structure (e.g, a tree)?

2. Does the problem get harder if we introduce attacking entities like wolves?

3. Can we come up with an algorithm that runs in polynomial time on instances where there is a valid winning sequence of constant length?

4. Is the problem hard even for a constant number of bunnies?

PS. Here’s a sketch of a slighty different reduction from vertex cover. Thanks again to Daniel for sharing the reduction described here! Comments welcome here, or continue the conversation on Twitter!