Tiling a Hexagon with Diamonds
A large regular hexagon is cut out of a triangular grid and tiled with diamonds (pairs of triangles glued together along an edge). Diamonds come in three varieties, depending on orientation; prove that precisely the same number of each variety must appear in the tiling.
Here’s the image demonstrating the grid and the individual tiles from the book cover:
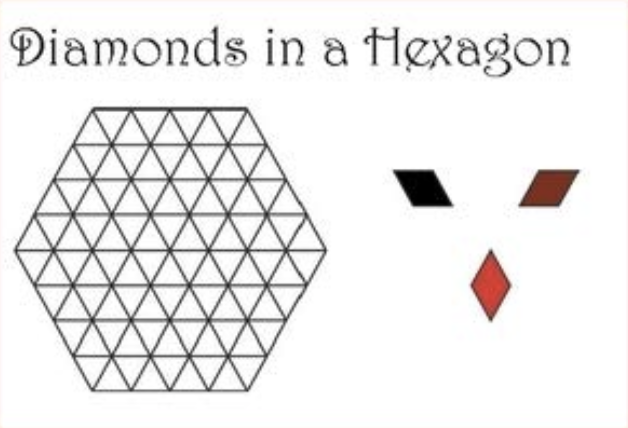
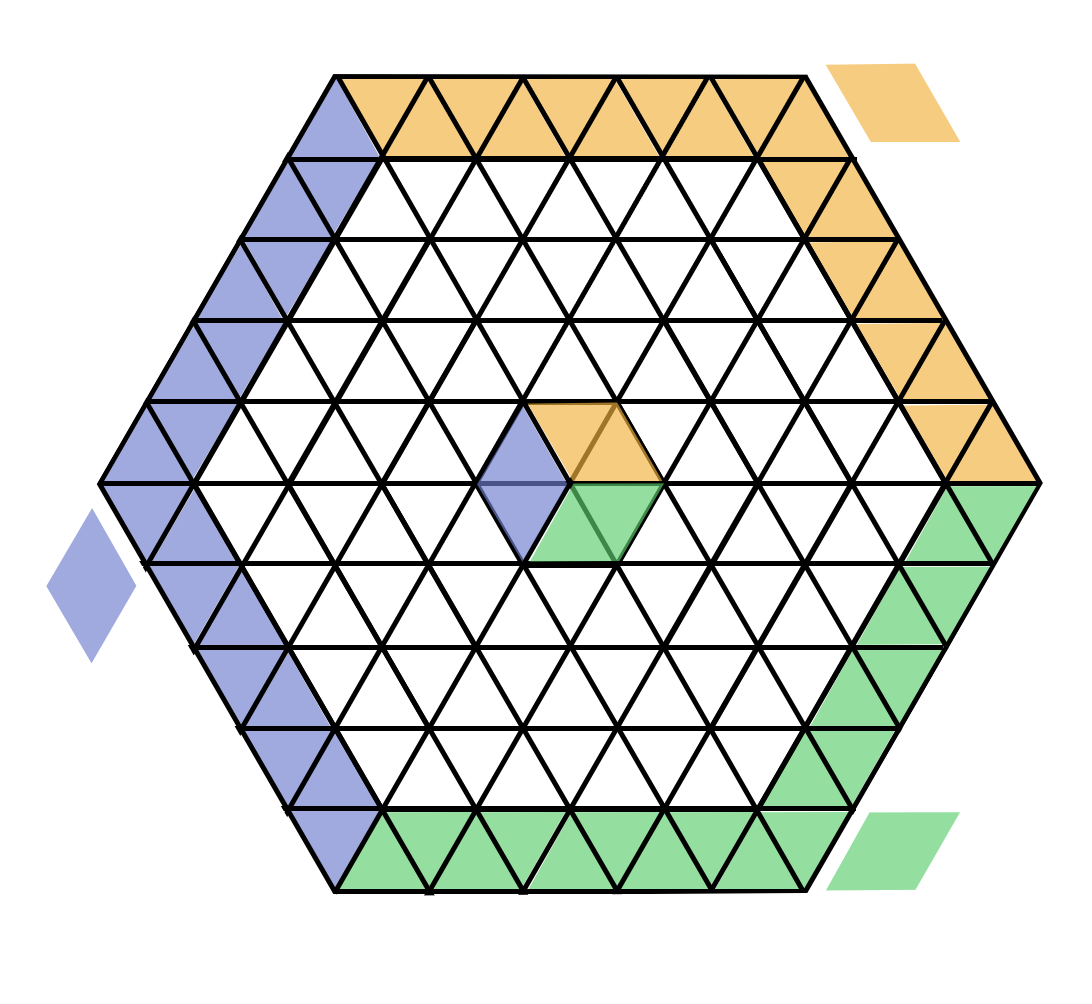
One attempt is to see if we can peel off layers using induction: the innermost hexagon in the partially color-coded image below corresponds to a base case of sorts; but it’s not clear how one might extend this approach — at least working with a c layers at a time for some constant c — since it’s not clear that every tiling can be split up as a combination of a complete tiling of c outermost layers and the rest.
Turns out that the image on the book’s front cover is a pretty cool hint!


