This course will explores the tradeoffs involved in coping with NP-completeness.
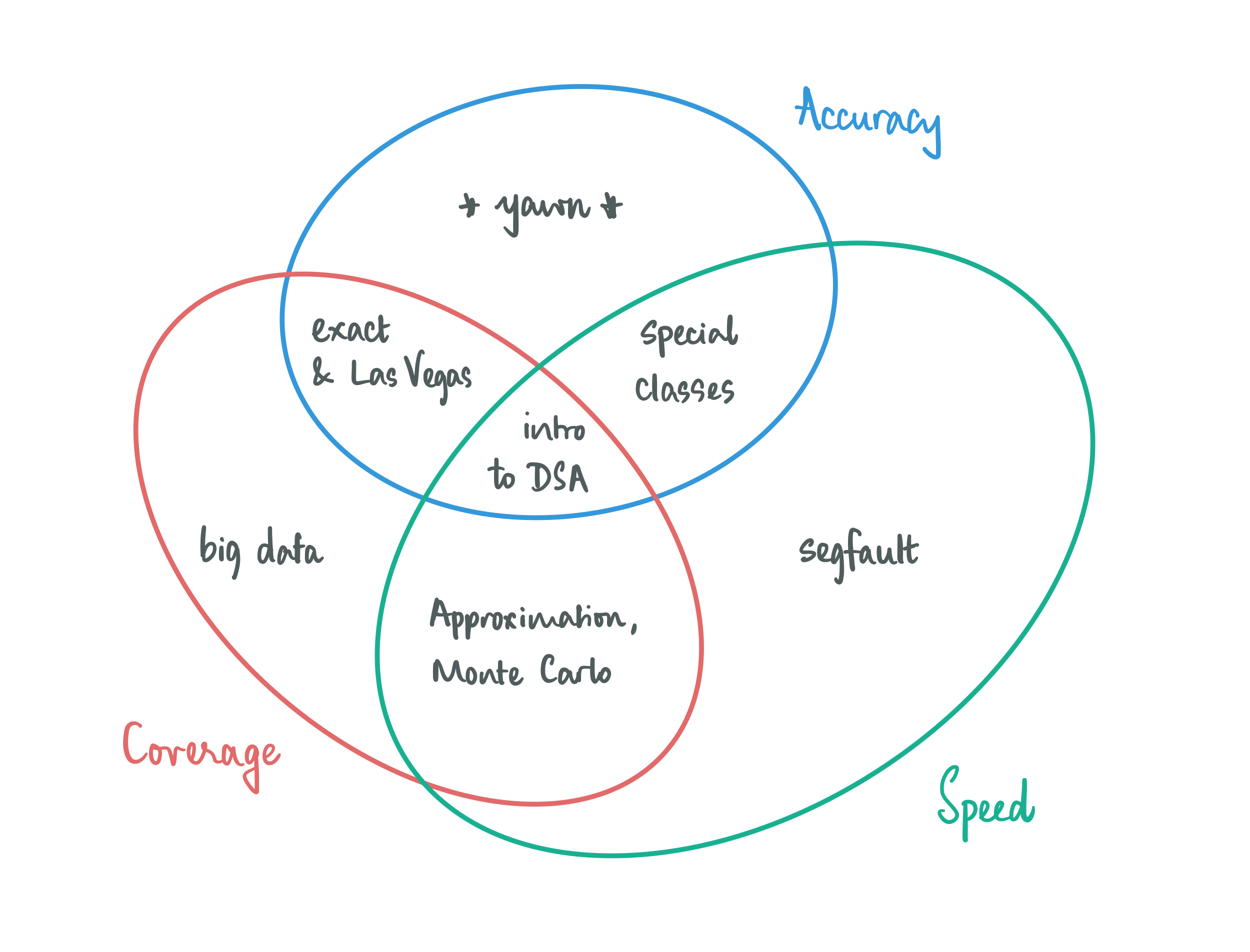
When we think about designing algorithms, we are usually very demanding in how we go about it: we require our algorithms to be fast and accurate on all conceivable inputs. This is asking for quite a bit, and perhaps it is not surprising that we cannot afford this luxury all the time. The good news is that most of the time we can make meaningful progress by relaxing just one of these demands:
Give up on accuracy, but not completely: look for solutions that are good enough (approximation) and/or work with algorithms that report the right solution most of the time (Las-Vegas style randomization).
Give up on coverage, a little bit: let your algorithms work well on structured inputs. Hopefully the structure is such that it is not too limiting and is interesting enough for some application scenario, and is also enough to give you algorithmic leverage, i.e, there’s enough that you can exploit to make fast and accurate algorithms.
Give up on speed, to some extent: going beyond the traditional allowance of polynomial time, which is the holy grail of what is considered efficient, takes you places. You could either allow for your algorithms have super-polynomial running times, and optimize as much as possible while being accurate on all inputs (exact algorithms), or allow for bad running times on a bounded subset of instances (Monte-Carlo style randomization).
This course is an introduction to techniques in achieving specific trade-offs, and understanding the theoretical foundations of frameworks that help us establish when certain tradeoffs are simply not feasible.