ES242. Data Structures and Algorithms I. Quiz 01

ES242. Data Structures and Algorithms I.

Quiz 01

Issued: 5 Jan, 2023

Back to course page

Problem 1. The 15-Puzzle

Suppose you are implementing the 15 puzzle game:

This is a sliding puzzle having 15 square tiles numbered 1–15 in a frame that is 4 tiles high and 4 tiles wide, leaving one unoccupied tile position. Tiles in the same row or column of the open position can be moved by sliding them horizontally or vertically, respectively. The goal of the puzzle is to rearrange the tiles and place them in increasing numerical order.

Here’s an example configuration:

An Example 15-Puzzle Instance

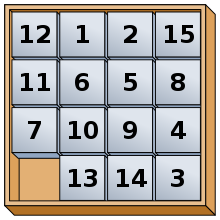
You decide to record the game state as a list of length 16, with elements between 0-15 (0 denotes the empty cell), using the following convention:

1. the first four elements contain the numbers in the first row of the board,

2. the fifth-eighth elements contain the numbers in the second row of the board,

3. the ninth-twelfth elements contain the numbers in the third row of the board, and

4. the thirteenth-sixteenth element csontain the numbers in the fourth row of the board.

Suppose you generalise this to a game involving a N \times N board, using a list of size N^2. The user indicates how they want to move at every step. Assume you can directly access and update any element in your list.

How much time do you need to update the configuration?

• proportional to N
• proportional to N^2
• constant

Problem 2. 2048

Suppose you are implementing the 2048 game:

2048 is played on a plain 4×4 grid, with numbered tiles that slide when a player moves them using the four arrow keys. Every turn, a new tile randomly appears in an empty spot on the board with a value of either 2 or 4. Tiles slide as far as possible in the chosen direction until they are stopped by either another tile or the edge of the grid. If two tiles of the same number collide while moving, they will merge into a tile with the total value of the two tiles that collided. The resulting tile cannot merge with another tile again in the same move.

Feel free to play the game at the link above to get a feel for it.

Suppose you are implementing a version of 2048 on a N \times N board, using a list of size N^2. As in the previous question, the list carries information about the state of the board: the first N elements correspond to the numbers in the first row, and so on. The user indicates in which direction they want to move at every step. Assume you can directly access and update any element in your list.

How much time do you need to update the configuration?

• proportional to N
• proportional to N^2
• constant

Problem 3. Game of Trust

Describe how to define a set of marriage preferences among n men and n women such that there is exactly one stable marriage possible.