ES242. Data Structures and Algorithms I. Quiz 01 Solutions

ES242. Data Structures and Algorithms I.

Quiz 01 Solutions

Released: 10 Jan, 2023

Problem 1. The 15-Puzzle

Suppose you are implementing the 15 puzzle game:

This is a sliding puzzle having 15 square tiles numbered 1–15 in a frame that is 4 tiles high and 4 tiles wide, leaving one unoccupied tile position. Tiles in the same row or column of the open position can be moved by sliding them horizontally or vertically, respectively. The goal of the puzzle is to rearrange the tiles and place them in increasing numerical order.

Here’s an example configuration:

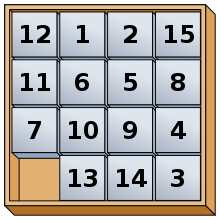
You decide to record the game state as a list of length 16, with elements between 0-15 (0 denotes the empty cell), using the following convention:

the first four elements contain the numbers in the first row of the board,
the fifth-eighth elements contain the numbers in the second row of the board,
the ninth-twelfth elements contain the numbers in the third row of the board, and
the thirteenth-sixteenth element csontain the numbers in the fourth row of the board.

Suppose you generalise this to a game involving a N \times N board, using a list of size N^2. The user indicates how they want to move at every step. Assume you can directly access and update any element in your list.

How much time do you need to update the configuration?

proportional to N
proportional to N^2
constant

Solution

Suppose the empty cell is at row R (counting from the top; i.e, the top row is row 1) and column C (counting from the left; i.e, the left-most column is column 1). The user may chose one of the following four moves:

move the number at row R-1 and column C into the empty cell, provided R is not the top row.
move the number at row R and column C-1 into the empty cell, provided C is not the left-most column.
move the number at row R and column C+1 into the empty cell, provided C is not the right-most column.
move the number at row R+1 and column C into the empty cell, provided R is not the bottom row.

The procedure to update the configuration involves two things:

identify the number to be moved into the empty slot based on the move chosen by the user;
update (swap) the values of the list at locations (R-1)*N + (C-1)¹ and the location corresponding to the number to be moved.

These two steps require knowledge of R and C, i.e, the location of the empty slot. Since we are given the contents of all locations as a list, we may need to — in the worst case — go through the entire list to find where the 0-element lies.

Note that to speed things up, we could store the integers R and C, representing the location of the 0-element, separately: and update it as moves are made. With this approach, the update can be achieved in constant time.

For this question, no such assumption is made, so the time required to update the configuration is proportional to N^2 in the worst-case.

Problem 2. 2048

Suppose you are implementing the 2048 game:

2048 is played on a plain 4×4 grid, with numbered tiles that slide when a player moves them using the four arrow keys. Every turn, a new tile randomly appears in an empty spot on the board with a value of either 2 or 4. Tiles slide as far as possible in the chosen direction until they are stopped by either another tile or the edge of the grid. If two tiles of the same number collide while moving, they will merge into a tile with the total value of the two tiles that collided. The resulting tile cannot merge with another tile again in the same move.

Feel free to play the game at the link above to get a feel for it.

Suppose you are implementing a version of 2048 on a N \times N board, using a list of size N^2. As in the previous question, the list carries information about the state of the board: the first N elements correspond to the numbers in the first row, and so on. The user indicates in which direction they want to move at every step. Assume you can directly access and update any element in your list.

How much time do you need to update the configuration?

proportional to N
proportional to N^2
constant

Solution

Notice that there are moves that may require that you update the status of every cell in the board (as an extreme example, suppose all the odd-numbered rows have elements in them and all the even-numbered rows are empty; and the user choses to move downwards: then except for possibly the bottom row have to be updated in a single move).

So one would have to examine the impact of the move on each cell in board and update all the cells, which requires time proportional to N^2.

Problem 3. Game of Trust

Describe how to define a set of marriage preferences among n men and n women such that there is exactly one stable marriage possible.

Solution

One situation where there is exactly one matching that is stable is when all the men and women have identical preferences. In particular, if we denote the set of n men as V := \{m_1,\ldots,m_n\} and the n women as W := \{w_1,\ldots,w_n\}, and further:

every man has the preference w_1 \succ w_2 \succ \cdots w_n and
every woman has the preference m_1 \succ m_2 \succ \cdots m_n;

then then only stable matching is (w_1,m_1),\cdots,(w_n,m_n).

To see this, suppose a stable matching M matches w_i to m_j where i \neq j, and let i be the smallest index for which this happens (i.e, for all \ell < i, M matches w_\ell with m_\ell). Then: it must be that j > i (since all men m_j with j < i are already matched to w_j). However, this implies that (w_i,m_i) will form a blocking pair (note that m_i is also matched to some w_t with t > i), contradicting our assumption that M is stable.

Food for thought: are there other examples?

Evaluation remark: for full credit, it suffices that the answer describes a valid example, even if there is no justification.

Footnotes

This assumes 0-based indexing; the exact index can be slightly different depending on convention.↩︎