191014K02 | Day 1 Lecture 1
191014K02: Day 1 Tutorial
Definitions
A c-approximate mincut is a set of at most cr edges if r is the number of edges in a mincut.
A minimum k-cut is a smallest set of edges whose removal would partition the graph to at least k connected components
The G(n, p) model, due to Erdös and Rényi, has two parameters, n and p. Here n is the number of vertices of the graph and p is the edge probability. For each pair of distinct vertices, v and w, p is the probability that the edge (v, w) is present. The presence of each edge is statistically independent of all other edges. The graph-valued random variable with these parameters is denoted by G(n, p). When we refer to “the graph G(n, p)”, we mean one realization of the random variable.
Problems
Generalize the mincut argument to c-approximate mincuts.
Generalize the mincut argument to min k-way cut.
Prove #min k-cuts is at most n^{O(k)}.
Show that G(n, 1/2) graphs have:
- many cliques of size 2 \log n-o(\log n) in expectation, and
- no cliques of size 2 \log n+o(\log n) in expectation (and with high probability).
Consider the following algorithm for finding a minimum cut. Assign a random score to each edge, and compute a minimum spanning tree. Removing the heaviest edge in the tree breaks it into two pieces. Argue that with probability \omega(1/n^2), those pieces will be the two sides of a minimum cut. Hint: relate this algorithm to the contraction algorithm we did in the class. Also think about Kruskal’s algorithm.
Show that for every n \geq 4, there is a simple graph G_n on n vertices that has at least {n \choose 2} distinct minimum cuts.
Show that for every n \geq 3, there is a simple graph G_n on n vertices such that the value of ILPOPT of the vertex cover ILP associated with G_n is at least one less than twice the value of LPOPT of the vertex cover LP associated with G_n, i.e:
\text{ILPOPT}(G_n) \geq 2\cdot \text{LPOPT}(G_n) - 1.
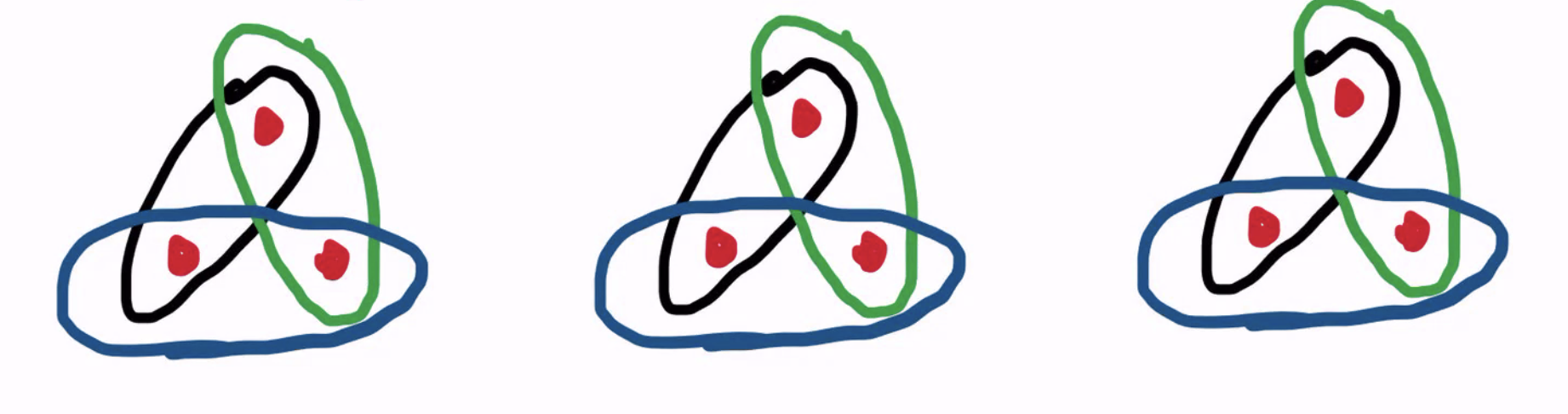
Consider the Set Cover instance shown in the figure below.
- Show that all-half is the unique LPOPT for this instance.
- Show that if you include every set in \mathcal{F}^\prime with probability x_s, then the probability that \mathcal{F}^\prime covers U is at most 2^{-\Omega(n)}.